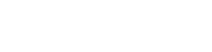大型语言模型（LLM）通常拥有数十亿参数，经过数万亿token的数据训练。然而，这样的模型训练和部署成本都非常昂贵。为了降低计算需求，人们常常采用各种模型压缩技术。
这些模型压缩技术一般可以分为四类：蒸馏、张量分解（包括低秩因式分解）、剪枝和量化。剪枝方法已经存在一段时间，但许多方法需要在剪枝后进行恢复微调（RFT）以保持性能，这使得整个过程成本高且难以扩展。
苏黎世联邦理工学院和微软的研究者提出了一个解决此问题的方法，名为SliceGPT。该方法的核心思想是通过删除权重矩阵中的行和列来降低网络的嵌入维数，以保持模型的性能。SliceGPT的出现为解决这一问题提供了一个有效的解决方案。
研究人员指出，借助SliceGPT，他们能够在几个小时内使用单个GPU对大型模型进行压缩，即使没有RFT，也能在生成和下游任务中保持有竞争力的性能。目前，该研究已被ICLR 2024接受。
- 论文标题：SLICEGPT: COMPRESS LARGE LANGUAGE MODELS BY DELETING ROWS AND COLUMNS
- 论文链接：https://arxiv.org/pdf/2401.15024.pdf
剪枝方法的工作原理是通过将LLM中的权重矩阵的某些元素设为零，并有选择地更新周围元素以进行补偿。这样可以形成一种稀疏模式，在神经网络的前向传递中跳过一些浮点运算，从而提高计算效率。
稀疏程度和稀疏模式是决定运算速度相对提升的因素。当稀疏模式更合理时，会带来更多的计算优势。与其他剪枝方法不同，SliceGPT使用切除（切掉！）权重矩阵的整行或整列的方式进行剪枝。在进行切除之前，网络会进行一次转换，以保持预测结果不变，但允许轻微影响的剪切过程。
结果是权重矩阵减小，信号传递减弱，神经网络维度降低。
下图 1 将 SliceGPT 方法与现有的稀疏性方法进行了比较。
通过大量实验，作者发现 SliceGPT 可以为 LLAMA-2 70B、OPT 66B 和 Phi-2 模型去除多达 25% 的模型参数（包括嵌入），同时分别保持密集模型 99%、99% 和 90% 的零样本任务性能。
经过 SliceGPT 处理的模型可以在更少的 GPU 上运行，而且无需任何额外的代码优化即可更快地运行：在 24GB 的消费级 GPU 上，作者将 LLAMA-2 70B 的推理总计算量减少到了密集模型的 64%；在 40GB 的 A100 GPU 上，他们将其减少到了 66%。
此外，他们还提出了一种新的概念，即 Transformer 网络中的计算不变性（computational invariance），它使 SliceGPT 成为可能。
SliceGPT 详解
SliceGPT 方法依赖于 Transformer 架构中固有的计算不变性。这意味着，你可以对一个组件的输出应用一个正交变换，只要在下一个组件中撤销即可。作者观察到，在网络区块之间执行的 RMSNorm 运算不会影响变换：这些运算是可交换的。
在论文中，作者首先介绍了在 RMSNorm 连接的 Transformer 网络中如何实现不变性，然后说明如何将使用 LayerNorm 连接训练的网络转换为 RMSNorm。接下来，他们介绍了使用主成分分析法（PCA）计算各层变换的方法，从而将区块间的信号投射到其主成分上。最后，他们介绍了删除次要主成分如何对应于切掉网络的行或列。
Transformer 网络的计算不变性
用 Q 表示正交矩阵：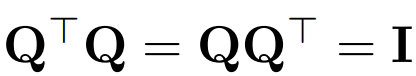
- 注意，向量 x 乘以 Q 不会改变向量的 norm，因为在这项工作中，Q 的维度总是与 transformer D 的嵌入维度相匹配。
假设 X_ℓ 是 transformer 一个区块的输出，经过 RMSNorm 处理后，以 RMSNorm (X_ℓ) 的形式输入到下一个区块。如果在 RMSNorm 之前插入具有正交矩阵 Q 的线性层，并在 RMSNorm 之后插入 Q^⊤，那么网络将保持不变，因为信号矩阵的每一行都要乘以 Q、归一化并乘以 Q^⊤。此处有：
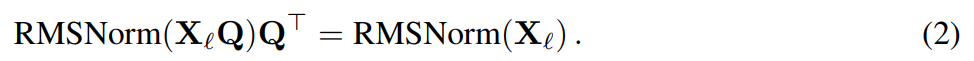
现在，由于网络中的每个注意力或 FFN 块都对输入和输出进行了线性运算，可以将额外的运算 Q 吸收到模块的线性层中。由于网络包含残差连接，还必须将 Q 应用于所有之前的层（一直到嵌入）和所有后续层（一直到 LM Head）的输出。
不变函数是指输入变换不会导致输出改变的函数。在本文的例子中，可以对 transformer 的权重应用任何正交变换 Q 而不改变结果，因此计算可以在任何变换状态下进行。作者将此称为计算不变性，并在下面的定理中加以定义。
定理 1：设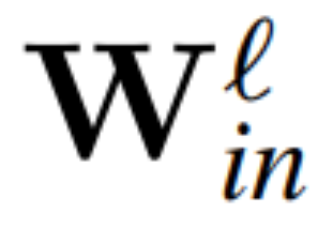 
和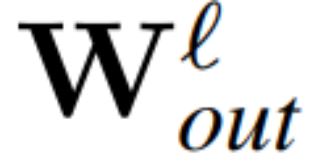
为 RMSNorm 连接的 transformer 网络第 ℓ 块线性层的权重矩阵，
、
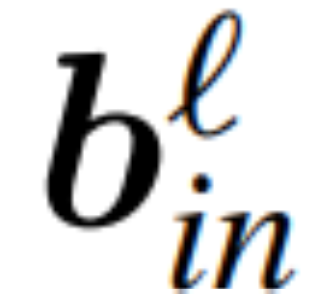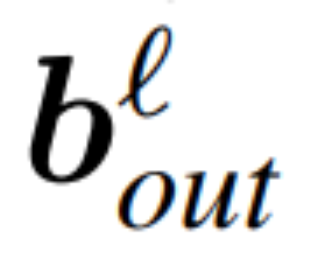为相应的偏置（如果有），W_embd 和 W_head 为嵌入矩阵和头矩阵。设 Q 是维数为 D 的正交矩阵，那么下面的网络就等同于原来的 transformer 网络：
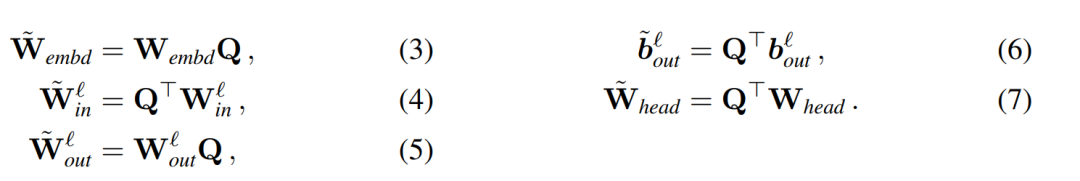
复制输入偏置和头偏置：
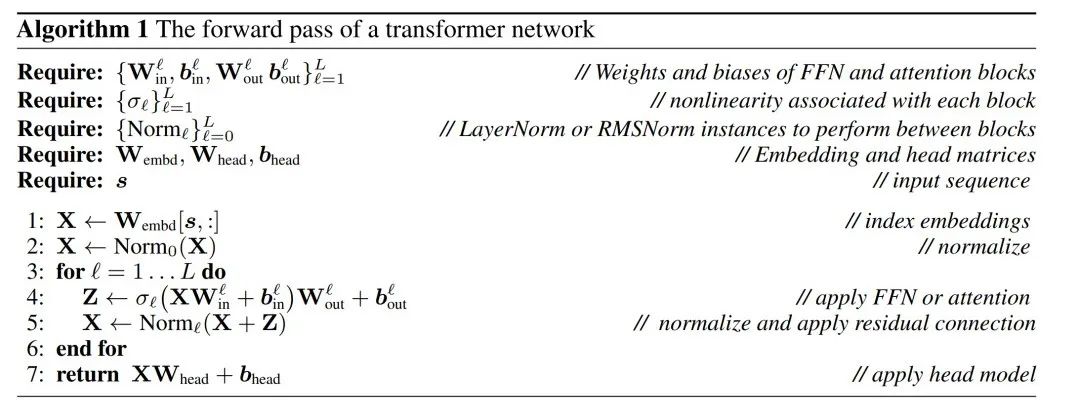
可以通过算法 1 来证明，转换后的网络计算出的结果与原始网络相同。
LayerNorm Transformer 可以转换为 RMSNorm
Transformer 网络的计算不变性仅适用于 RMSNorm 连接的网络。在处理使用 LayerNorm 的网络之前，作者先将 LayerNorm 的线性块吸收到相邻块中，从而将网络转换为 RMSNorm。
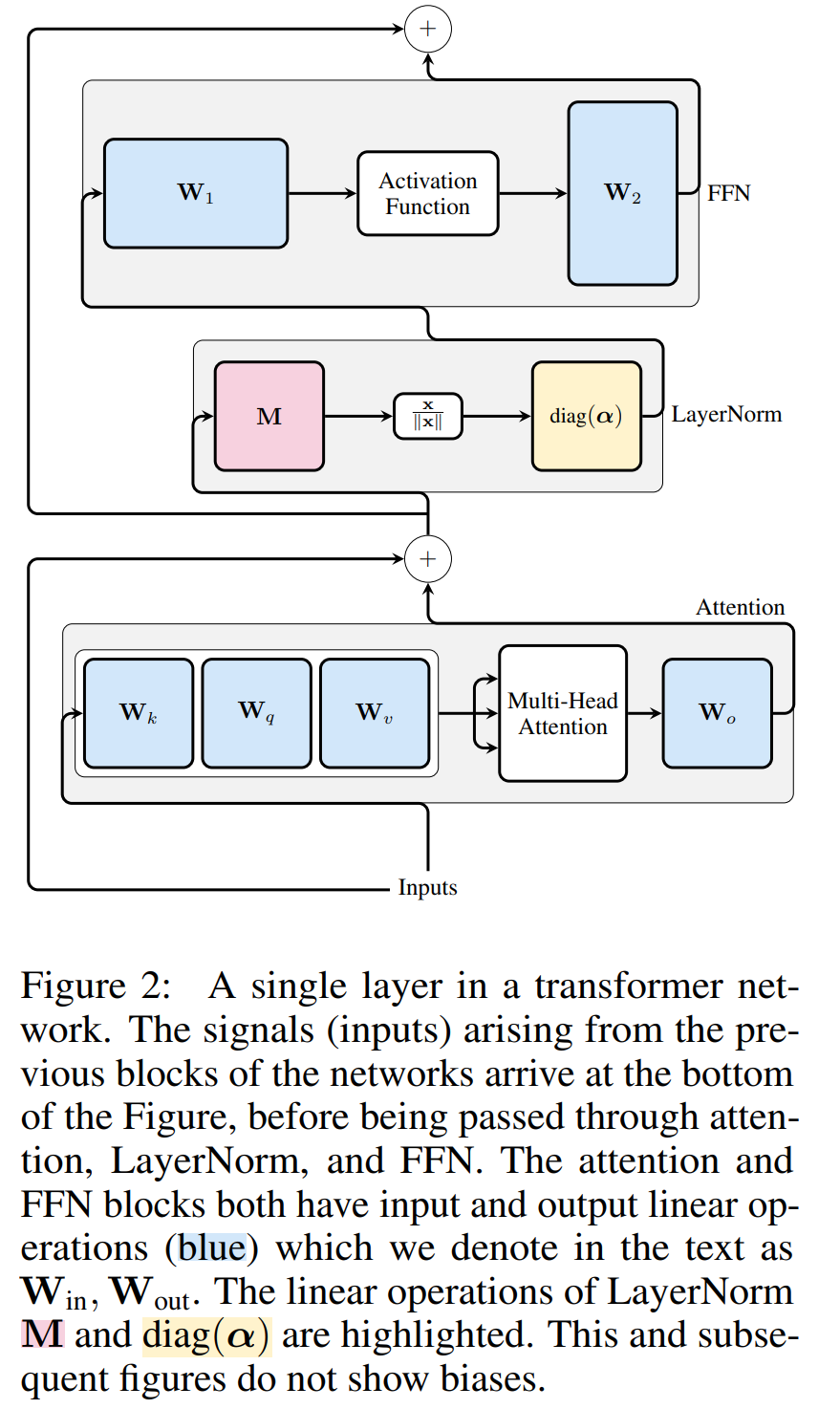
图 3 显示了 Transformer 网络（见图 2）的这种转换。在每个区块中，作者将输出矩阵 W_out 与均值减法矩阵 M 相乘，后者考虑了后续 LayerNorm 中的均值减法。输入矩阵 W_in 被前面 LayerNorm 块的比例预乘。嵌入矩阵 W_embd 必须进行均值减法，而 W_head 必须按照最后一个 LayerNorm 的比例重新缩放。这只是运算顺序的简单改变，不会影响网络输出。
每个块的转换
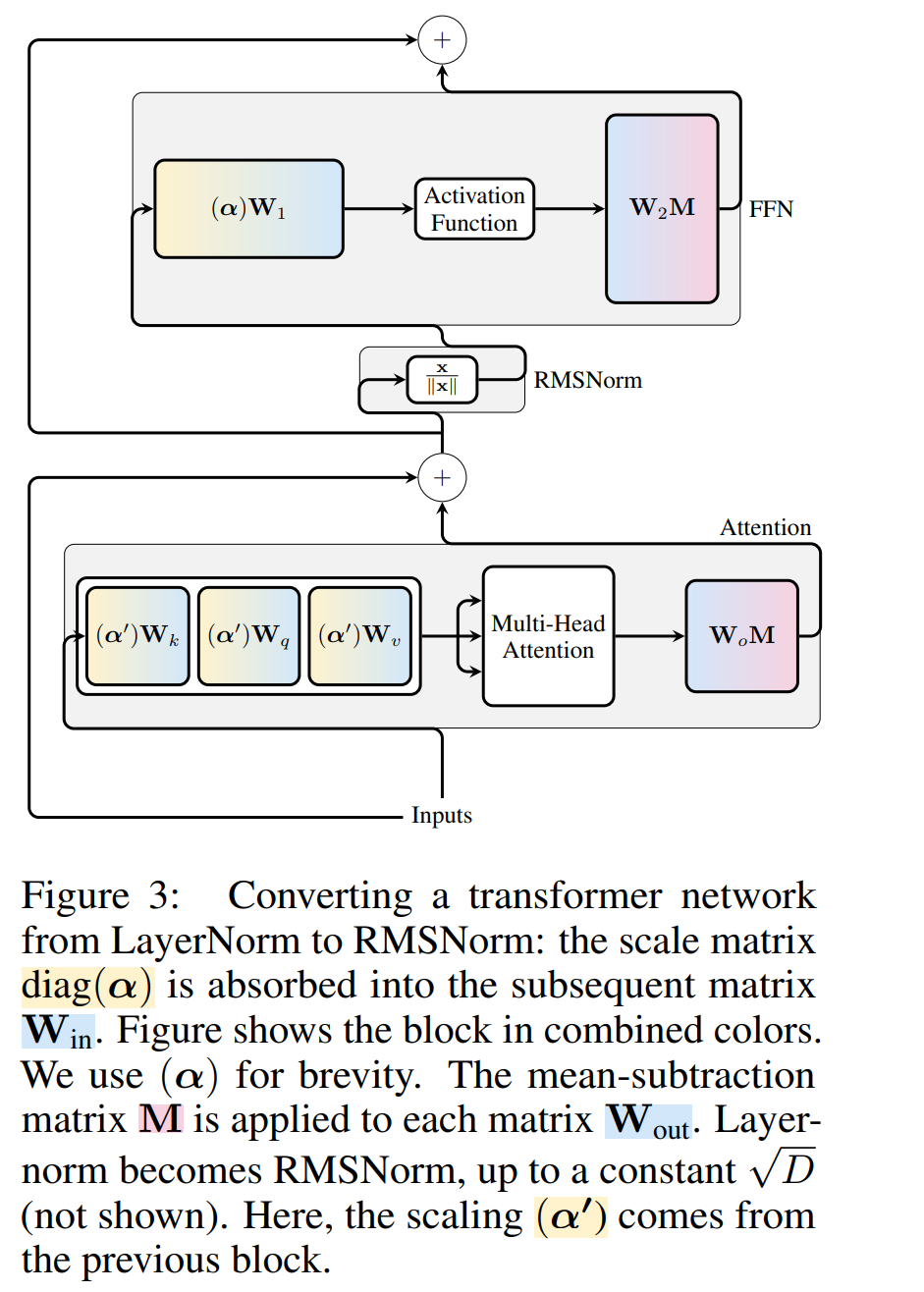
现在 transformer 中的每个 LayerNorm 都已转换为 RMSNorm，可以选择任意 Q 来修改模型。作者最初的计划是从模型中收集信号，利用这些信号构建一个正交矩阵，然后删除部分网络。他们很快发现，网络中不同区块的信号并没有对齐，因此他们需要在每个区块应用不同的正交矩阵，即 Q_ℓ。
如果每个区块使用的正交矩阵不同，则模型不会改变，证明方法与定理 1 相同，但算法 1 第 5 行除外。在这里可以看到，残差连接和块的输出必须具有相同的旋转。为了解决这个问题，作者通过对残差进行线性变换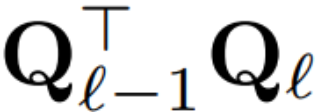 
来修改残差连接。
图 4 显示了如何通过对残差连接进行额外的线性运算，对不同的区块进行不同的旋转。与权重矩阵的修改不同，这些附加运算无法预先计算，并且会给模型增加少量（D × D）开销。尽管如此，还是需要通过这些操作来对模型进行切除操作，而且可以看到整体速度确实加快了。
为了计算矩阵 Q_ℓ，作者使用了 PCA。他们从训练集中选择一个校准数据集，在模型中运行（在将 LayerNorm 运算转换为 RMSNorm 之后），并提取该层的正交矩阵。更确切地说，如果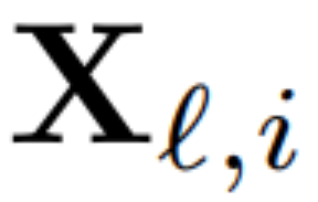 
他们使用转换后网络的输出来计算下一层的正交矩阵。更确切地说，如果 
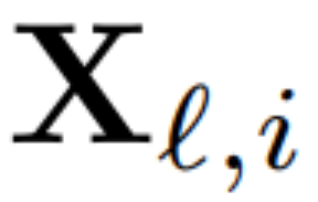是校准数据集中第 i 个序列的第 ℓ 个 RMSNorm 模块的输出，计算：
并将 Q_ℓ设为 C_ℓ 的特征向量，按特征值递减排序。
切除
主成分分析的目标通常是获取数据矩阵 X 并计算低维表示 Z 和近似重构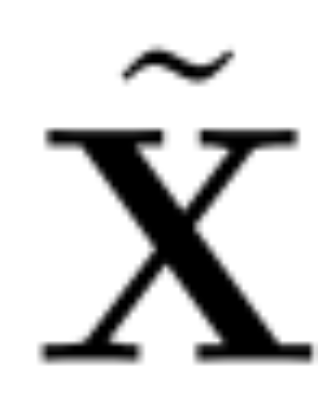
：
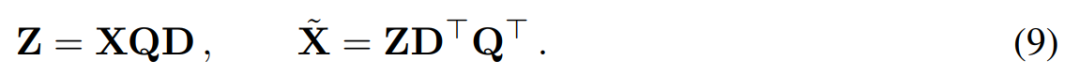
其中 Q 是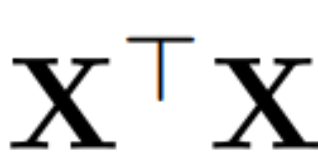 
的特征向量，D 是一个 D × D 小删除矩阵（包含 D × D 同位矩阵的 D 小列），用于删除矩阵左边的一些列。从 QD 是最小化 
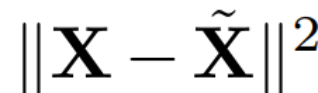的线性映射的意义上来说，重建是 L_2 最佳（L_2 optimal）的。
当对区块间的信号矩阵 X 应用 PCA 时，作者从未将 N × D 信号矩阵具体化，而是将删除矩阵 D 应用于构建该矩阵前后的运算。在上述运算中，该矩阵已乘以 Q。作者删除了 W_in 的行以及 W_out 和 W_embd 的列。他们还删除了插入到残差连接中的矩阵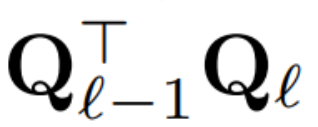 
的行和列（见图 4）。
实验结果
生成任务
作者对经过 SliceGPT 和 SparseGPT 剪裁后大小不同的 OPT 和 LLAMA-2 模型系列在 WikiText-2 数据集中进行了性能评估。表 1 展示了模型经过不同级别的剪裁后保留的复杂度。相比 LLAMA-2 模型，SliceGPT 在应用于 OPT 模型时表现出了更优越的性能，这与作者根据模型频谱的分析得出的推测相符。
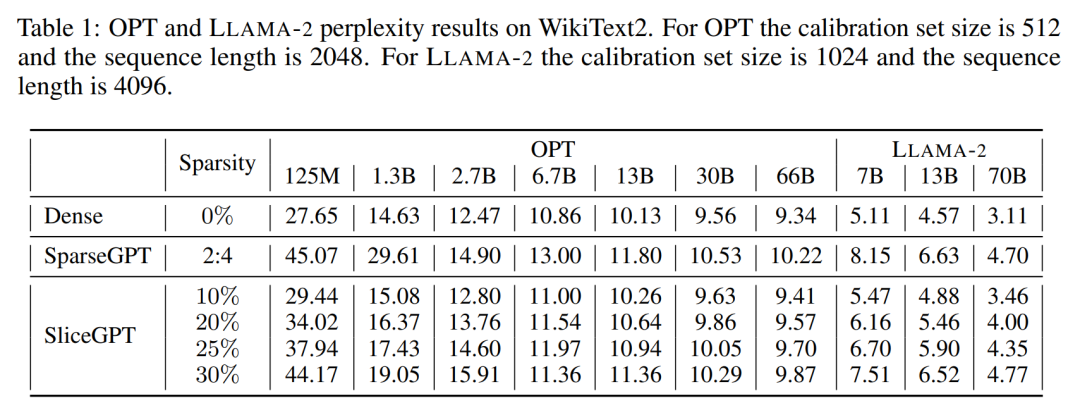
SliceGPT 的性能将随着模型规模的增大而提升。在对所有 LLAMA-2 系列模型剪裁 25% 情况下，SparseGPT 2:4 模式的表现都逊于 SliceGPT。对于 OPT，可以发现在除 2.7B 模型之外的所有模型中，30% 切除比例的模型的稀疏性都优于 2:4 的稀疏性。
零样本任务
作者采用了 PIQA、WinoGrande、HellaSwag、ARC-e 和 ARCc 五个任务来评估 SliceGPT 在零样本任务上的表现，他们在评估中使用了 LM Evaluation Harness 作为默认参数。
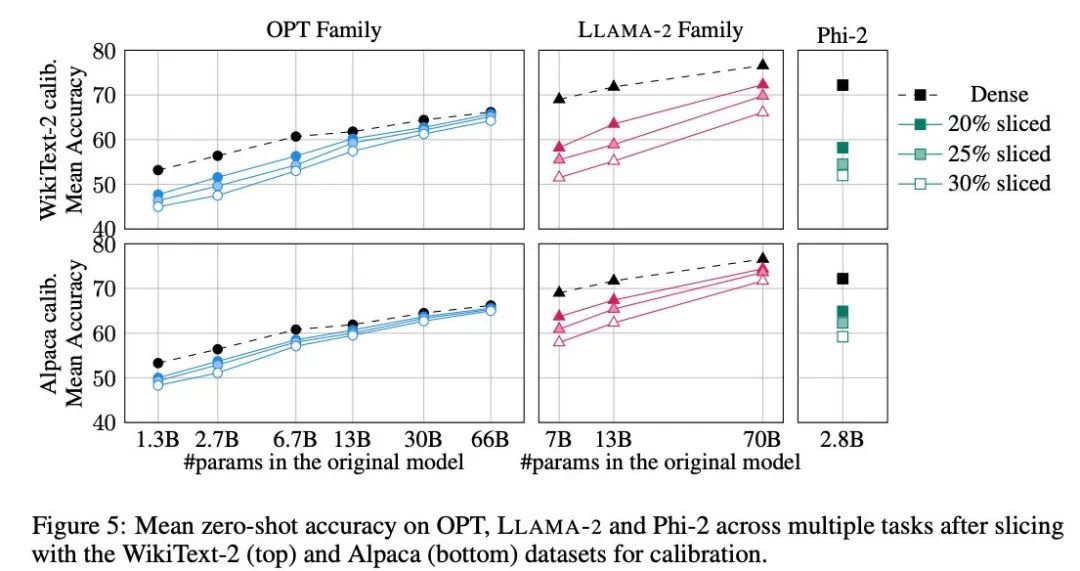
图 5 展示了经过剪裁的模型在以上任务中取得的平均分数。图中上行显示的是 SliceGPT 在 WikiText-2 中的平均准确率，下行显示的是 SliceGPT 在 Alpaca 的平均准确率。从结果中可以观察到与生成任务中类似的结论：OPT 模型比 LLAMA-2 模型更适应压缩，越大的模型经过剪裁后精度的下降越不明显。
作者在 Phi-2 这样的小模型中测试了 SliceGPT 的效果。经过剪裁的 Phi-2 模型与经过剪裁的 LLAMA-2 7B 模型表现相当。最大型的 OPT 和 LLAMA-2 模型可以被有效压缩，当从 66B 的 OPT 模型中删除 30% 时，SliceGPT 可以做到仅损失了几个百分点。
作者还进行了恢复微调（RFT）实验。使用 LoRA 对剪裁过的 LLAMA-2 和 Phi-2 模型进行了少量 RFT。
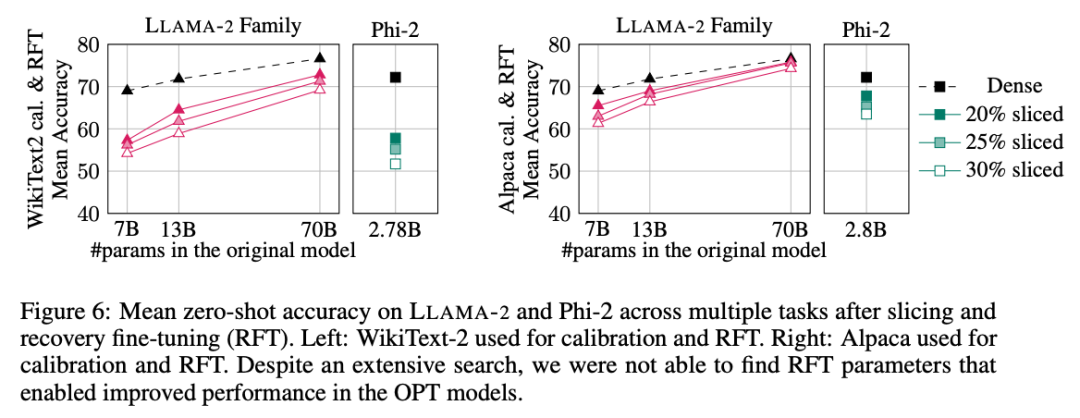
实验结果如图 6 所示。可以发现，RFT 的结果在 WikiText-2 和 Alpaca 数据集存在显著差异，模型在 Alpaca 数据集中展现了更好的性能。作者认为出现差异的原因在于 Alpaca 数据集中的任务和基准任务更接近。
对于规模最大的 LLAMA-2 70B 模型，剪裁 30% 再进行 RFT 后，最终在 Alpaca 数据集中的平均准确率为 74.3%，原稠密模型的准确率为 76.6%。经过剪裁的模型 LLAMA-2 70B 保留了约 51.6B 个参数，其吞吐量得到了显著提高。
作者还发现 Phi-2 无法在 WikiText-2 数据集中，从被剪裁过的模型中恢复原有准确率，但在 Alpaca 数据集中能恢复几个百分点的准确率。被剪裁过 25% 并经过 RFT 的 Phi-2 在 Alpaca 数据集中，平均准确率为 65.2%，原稠密模型的准确率为 72.2%。剪裁过的模型保留了 2.2B 个参数，保留了 2.8B 模型准确率的 90.3%。这表明即使是小型语言模型也可以有效剪枝。
基准吞吐量
和传统剪枝方法不同，SliceGPT 在矩阵 X 中引入了（结构化）稀疏性：整列 X 被切掉，降低了嵌入维度。这种方法既增强了 SliceGPT 压缩模型的计算复杂性（浮点运算次数），又提高了数据传输效率。
在 80GB 的 H100 GPU 上，将序列长度设置为 128，并将序列长度批量翻倍找到最大吞吐量，直到 GPU 内存耗尽或吞吐量下降。作者比较了剪裁过 25% 和 50% 的模型的吞吐量与原稠密模型 80GB 的 H100 GPU 上的吞吐量。剪裁过 25% 的模型最多实现了 1.55 倍的吞吐量提升。
在剪裁掉 50% 的情况下，最大的模型在使用一个 GPU 时，吞吐量实现了 3.13 倍和 1.87 倍的大幅增加。这表明在 GPU 数量固定的情况下，被剪裁过的模型的吞吐量将分别达到原稠密模型的 6.26 倍和 3.75 倍。
经过 50% 的剪裁后，虽然 SliceGPT 在 WikiText2 中的保留的复杂度比 SparseGPT 2:4 差，但吞吐量却远超 SparseGPT 的方法。对于大小为 13B 的模型，在内存较少的消费级 GPU 上，小模型的吞吐量可能也会有所提高。
推理时间
作者还研究了使用 SliceGPT 压缩的模型从端到端的运行时间。表 2 比较了在 Quadro RTX6000 和 A100 GPU 上，OPT 66B 和 LLAMA-2 70B 模型生成单个 token 所需的时间。可以发现，在 RTX6000 GPU 上，对模型剪裁过 25% 后，推理速度提高了 16-17%；在 A100 GPU 上，速度提高了 11-13%。相比原稠密模型，对于 LLAMA-2 70B，使用 RTX6000 GPU 所需的计算量减少了 64%。作者将这种提升归功于 SliceGPT 采用了用较小的权重矩阵替换原权重矩阵，并使用了 dense kernels ，这是其他剪枝方案无法实现的。
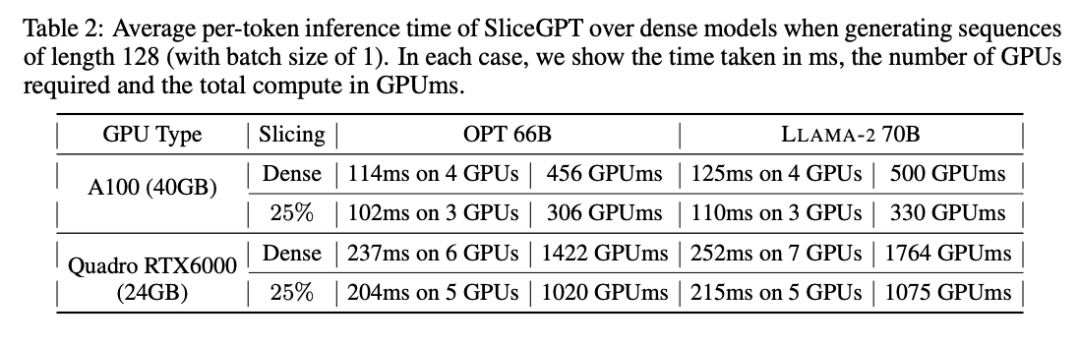
作者表示，在撰写本文时，他们的基线 SparseGPT 2:4 无法实现端到端的性能提升。相反，他们通过比较 transformer 层中每个运算的相对时间，将 SliceGPT 与 SparseGPT 2:4 进行比较。他们发现，对于大型模型，SliceGPT (25%) 与 SparseGPT (2:4) 在速度提升和困惑度方面具有竞争力。
计算成本
所有 LLAMA-2、OPT 和 Phi-2 模型都可以在单个 GPU 上花费 1 到 3 小时的时间进行切分。如表 3 所示，通过恢复微调，可以在 1 到 5 个小时内压缩所有 LM。
了解更多内容，请参考原论文。
