核模型高斯过程(KMGPs)是一种复杂的工具,用于处理各种数据集的复杂性。它通过核函数扩展了传统高斯过程的概念。本文将详细讨论KMGPs的理论基础、实际应用和面临的挑战。
核模型高斯过程是对传统高斯过程的一种扩展,用于机器学习和统计学。了解kmgp前,需掌握高斯过程基础知识,再理解核模型的作用。
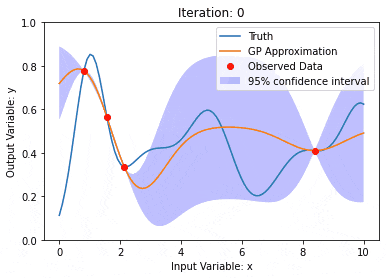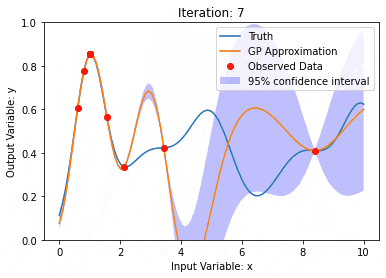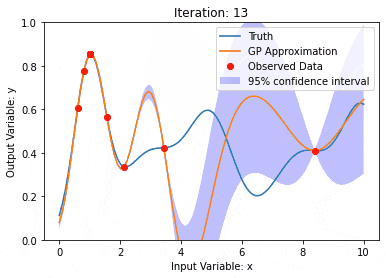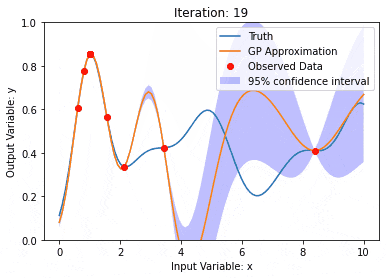
高斯过程(GPs)
高斯过程是随机变量集合,有限个变量联合高斯分布,用于定义函数概率分布。
高斯过程在机器学习中常用于回归和分类任务,可用于拟合数据的概率分布。
高斯过程的一个重要特征是能够提供不确定性估计和预测,这在理解预测可信度与预测本身同样重要的任务中非常有用。
核函数建模
在高斯过程中,核函数(或协方差函数)被用来衡量不同数据点之间的相似性。核函数接收两个输入并计算它们之间的相似度分数。
有各种类型的核,例如线性、多项式和径向基函数(RBF)。每个核都有不同的特点,可根据问题选择适合的核。
在高斯过程中,核建模是选择和优化核函数,以最佳地捕捉数据中的底层模式的过程。这一步骤非常重要,因为核的选择和配置会显著影响高斯过程的性能。
核模型高斯过程(KMGPs)
KMGPs是标准GP(高斯过程)的扩展,专注于核函数的应用。与标准GP相比,KMGPs更加注重根据特定类型的数据或问题定制复杂或定制设计的核函数。这种方法在数据复杂且标准核函数无法捕捉底层关系的情况下特别有用。然而,在KMGPs中设计和调优核函数是具有挑战性的,通常需要在问题领域和统计建模方面具有深厚的领域知识和专业经验。
核模型高斯过程是统计学习中的一个复杂工具,提供了一种灵活而强大的方法来建模复杂的数据集。它们因其提供不确定性估计的能力以及通过自定义核对不同类型数据的适应性而受到特别重视。
KMGP中设计良好的内核可以对数据中的非线性趋势、周期性和异方差(变化的噪声水平)等复杂现象进行建模。所以需要深入的领域知识和对统计建模的透彻理解。
KMGP在许多领域都有应用。在地质统计学中,他们对空间数据进行建模,捕捉潜在的地理变化。在金融领域,它们被用来预测股票价格,解释了金融市场不稳定和复杂的本质。在机器人和控制系统中,KMGPs在不确定情况下对动态系统的行为进行建模和预测。
代码
我们使用合成数据集创建一个完整的Python代码示例,这里用到一个库GPy,它是python中专门处理高斯过程的库。
pip install numpy matplotlib GPy
导入库
import numpy as np import matplotlib.pyplot as plt import GPy
然后我们将使用numpy创建一个合成数据集。
X = np.linspace(0, 10, 100)[:, None] Y = np.sin(X) + np.random.normal(0, 0.1, X.shape)
使用GPy定义和训练高斯过程模型
kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.) model = GPy.models.GPRegression(X, Y, kernel) model.optimize(messages=True)
在训练模型后,我们将使用它对测试数据集进行预测。然后绘制图表可视化模型的性能。
X_test = np.linspace(-2, 12, 200)[:, None] Y_pred, Y_var = model.predict(X_test) plt.figure(figsize=(10, 5)) plt.plot(X_test, Y_pred, 'r-', lw=2, label='Prediction') plt.fill_between(X_test.flatten(), (Y_pred - 2*np.sqrt(Y_var)).flatten(), (Y_pred + 2*np.sqrt(Y_var)).flatten(), alpha=0.5, color='pink', label='Confidence Interval') plt.scatter(X, Y, c='b', label='Training Data') plt.xlabel('X') plt.ylabel('Y') plt.title('Kernel Modeled Gaussian Process Regression') plt.legend() plt.show()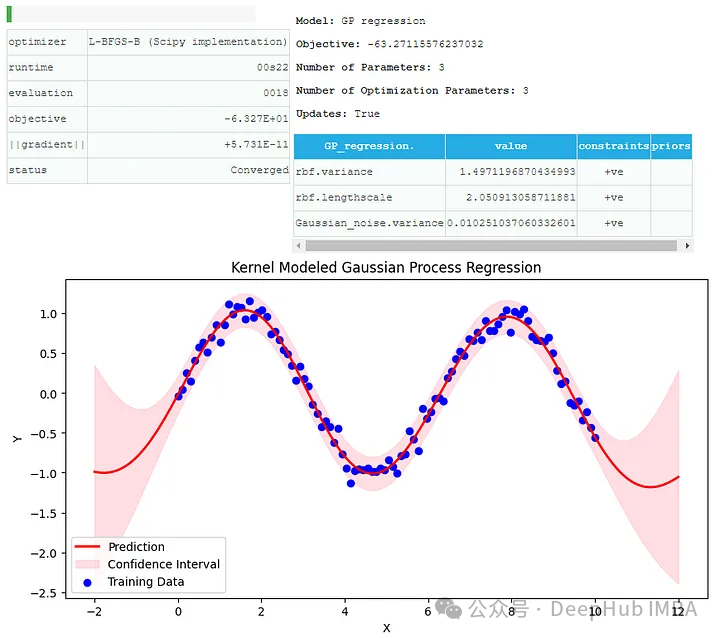
我们这里应用带有RBF核的高斯过程回归模型,可以看到预测与训练数据和置信区间。
总结
核模型高斯过程代表了统计学习领域的重大进步,为理解复杂数据集提供了灵活而强大的框架。GPy也包含了基本上我们能看到的所有的核函数,以下是官方文档的截图:
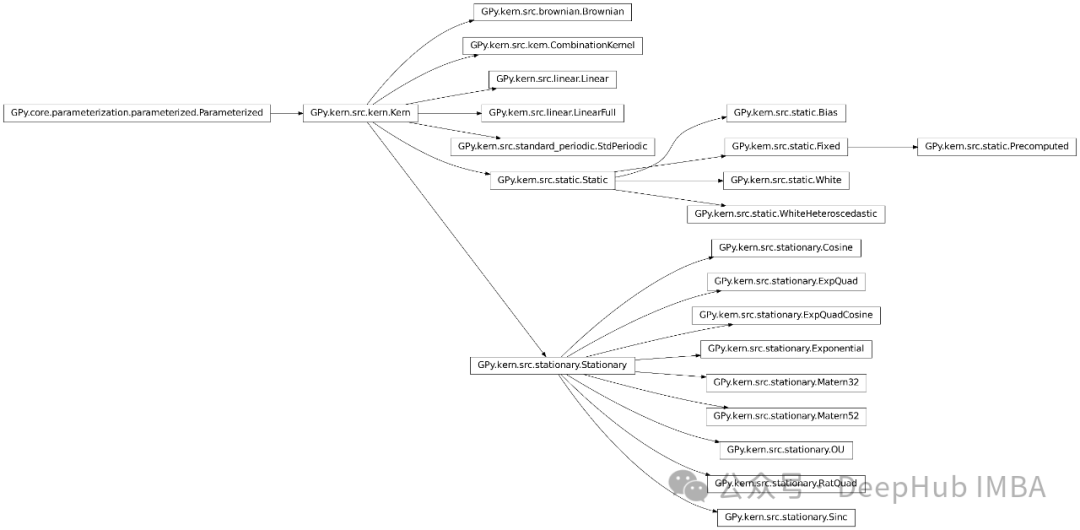
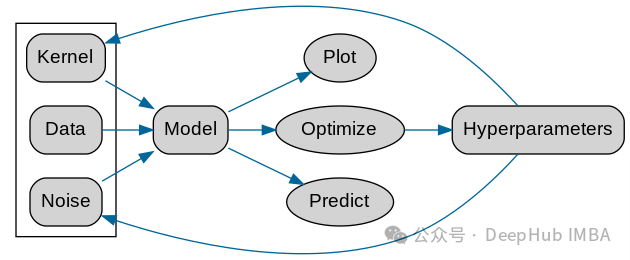
针对于不同的数据会需要选择不同的核函数核超参数,这里GPy官方也给出了一个流程图